Degrees of Freedom

Overview

Teaching: 10 min
Exercises: 0 min

Questions

• How is kinetic energy contained and distributed in a dynamic molecular system

• How to increase efficiency of thermodynamic sampling

• How reduction of degrees of freedom affects dynamics

Objectives

• Explain how kinetic energy is distributed in a simulation system

• Understand how to correctly increase efficiency of thermodynamic sampling

Molecular degrees of freedom

Molecular degrees of freedom refer to the number of unique ways a molecule may move (increase its kinetic energy). Thus the molecular degrees of freedom describe how kinetic energy is contained and distributed in a molecule. Dynamical molecular systems are characterized by numerous degrees of freedom. The motion of molecules can be decomposed into translational, rotational, and vibrational components.

• The number of unique ways a molecule may move (increase its kinetic energy).
• Describe how kinetic energy is contained and distributed in a molecule.
• Translational, rotational, and vibrational components.

Equipartition theorem

On average, when thermal energy is added to a system, the energy is shared equally among the degrees of freedom (equipartition theorem). In other words, classical equipartition principle states that every (quadratic) degree of freedom contributes equally to the total energy in thermal equilibrium. Each degree of freedom has an average energy of \(\frac{1}{2}k_BT\) and contributes \(\frac{1}{2}k_B\) to the system’s heat capacity.

• The energy is shared equally among the degrees of freedom (equipartition theorem).
• Each degree of freedom has an average energy of \(\frac{1}{2}k_BT\) and contributes \(\frac{1}{2}k_B\) to the system’s heat capacity.

Degrees of freedom and thermodynamics properties

When the same amount of kinetic energy flows into simulation systems containing different types of molecules, their temperature will change by a different amount. The more places (degrees of freedom) there are to put the energy the less the temperature change will be.

The number of degrees of freedom is an important quantity allowing us to estimate various thermodynamic properties of a simulation system such as heat capacity, entropy, temperature.

Translational degrees of freedom

An atom or a molecule can move in three dimensions. Thus, any atom or molecule has three degrees of freedom associated with translational motion of the center of mass with respect to the X, Y, and Z axes.

• The three translational degrees of freedom in three dimensions provide \(\frac{3}{2}k_BT\) of energy.

Rotational degrees of freedom

From the classical point of view atoms have a negligible amount of rotational energy because their mass is concentrated in the nucleus. Since radius of a nucleus is about \(10^{-15}\) m, atoms have negligible rotational moment of inertia. (From the QM point of view rotation of an atom has no meaning because such rotations lead to configurations which are indistinguishable from the original configuration). But molecules are different in this respect, they can have rotational kinetic energy. A linear molecule, has two rotational degrees of freedom, because it can rotate about either of two axes perpendicular to the molecular axis. The rotations along the molecular axis have a negligible amount of rotational energy because the mass is concentrated very close to the axis of rotation. A nonlinear molecule, where the atoms do not lie along a single axis, like water, has three rotational degrees of freedom, because it can rotate around any of three perpendicular axes.

• The rotational degrees of freedom contribute \(k_BT\) to the energy of linear molecules and \(\frac{3}{2}k_BT\) to the energy of non-linear molecules.

• Atoms have a negligible amount of rotational energy because their mass is concentrated in the nucleus which is very small (about \(10^{-15}\) m).
• A linear molecule, has two rotational degrees of freedom.
• A nonlinear molecule, where the atoms do not lie along a single axis, has three rotational degrees of freedom, because it can rotate around any of three perpendicular axes.
• The rotational degrees of freedom contribute \(k_BT\) to the energy of linear molecules and \(\frac{3}{2}k_BT\) to the energy of non-linear molecules.

Vibrational degrees of freedom

A molecule can also vibrate. A diatomic molecule has one molecular vibration mode, where the two atoms oscillate back and forth with the chemical bond between them acting as a spring.

A molecule with N atoms has more complicated modes of molecular vibration, with 3N − 5 vibrational modes for a linear molecule and 3N − 6 modes for a nonlinear molecule. (Linear molecules can bend it two orthogonal planes).

• A diatomic molecule has one molecular vibration mode.
• A linear molecule with N atoms has 3N − 5 vibrational modes.
• A non-linear molecule with N atoms has 3N − 6 vibrational modes.

Angle bend	Symmetric stretch	Asymmetric stretch

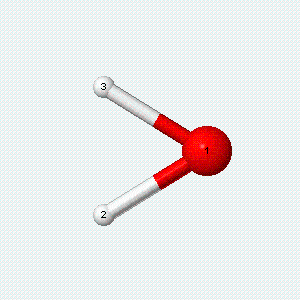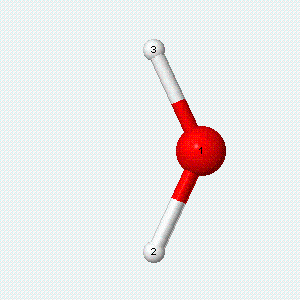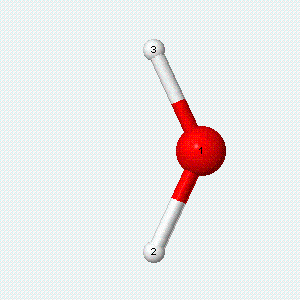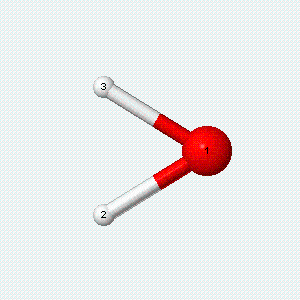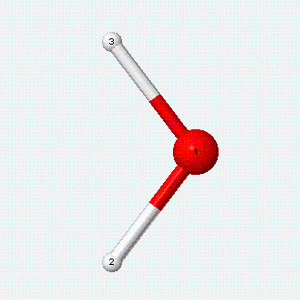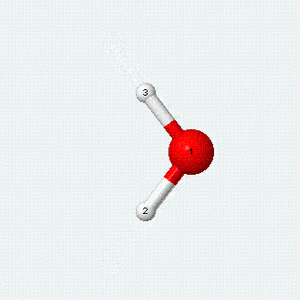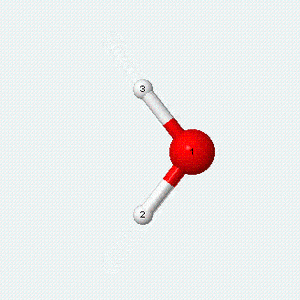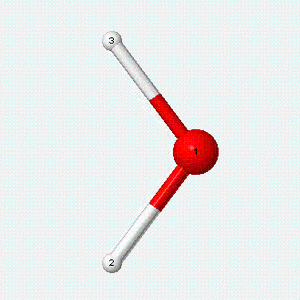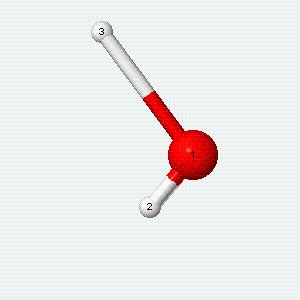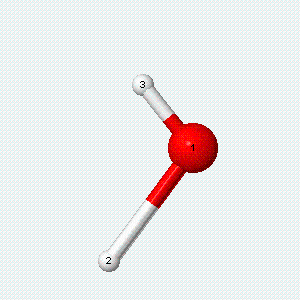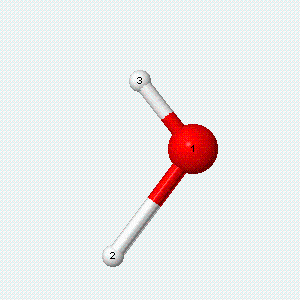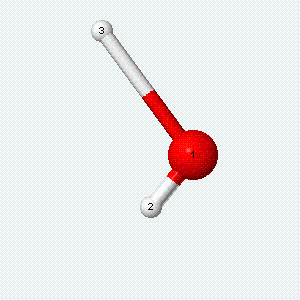Each vibrational mode has two degrees of freedom for energy: the kinetic energy of moving atoms is one degree of freedom, and the potential energy of spring-like chemical bonds is another.

Each vibrational degree of freedom provides \(k_BT\) of energy. However, this is valid only when \(k_BT\) is much bigger than spacing between vibrational states. At low temperature this condition is not satisfied, only a few vibrational states are occupied and the equipartition principle is not typically applicable.

• There are two degrees of freedom for each vibrational mode.
• One degree involves the kinetic energy of the moving atoms, and the other involves the potential energy of the springlike chemical bond(s).
• Each vibrational degree of freedom contributes \(k_BT\) to the energy of a molecule. However, this is valid only when \(k_BT\) is much bigger than energy spacing between vibrational modes.
• At low temperature this condition is not satisfied, only a few vibrational states are occupied and the equipartition principle is not typically applicable.

Increasing efficiency of thermodynamic sampling.

To compute thermodynamic quantities with a molecular simulation, we sample a configuration space with the dimensionality determined by the number of degrees of freedom. Thus, by reducing the number of degrees of freedom (of course when physically justifiable) we can increase thermodynamic sampling efficiency.

By removing the fastest degrees of freedom, we can increase the integration time step. Bond constraints, for example, make it possible to use longer time steps by eliminating rapid vibrational modes. The degrees of freedom associated with angles and torsions can also be eliminated by applying constraints to allow further increase of the integration step.

Using coarse-grained models, complex systems can be simplified by reducing their degrees of freedom. By averaging interactions across groups of particles, coarse-grained models capture essential features while minimizing computational costs.

Reduction of the number of degrees of freedom may lead to artifacts.

Adding constraints, however, can affect simulation dynamics by restricting motions associated with the eliminated degrees of freedom. For example it was found that bond and angle constraints slow down dihedral angle transitions (Toxvaerd, 1987), shift the frequencies of the normal modes in biomolecules (Tobias and Brooks, 1988), and perturb the dynamics of polypeptides (Hinsen and Kneller, 1995).

Coarse-grained modeling also affects simulation dynamics. It produces approximate dynamics by sacrificing atomic details.

In conclusion, choosing the right number of degrees of freedom depends on the balance between accuracy and computational efficiency.

• If there are too few degrees of freedom, the simulation will be approximate
• If there are too many degrees of freedom the computation will be prohibitively slow.

Bond and angle constraints can:

• slow down dihedral angle transitions [1]
• shift the frequencies of the normal modes in biomolecules [2]
• perturb the dynamics of polypeptides [3].

Key Points

• Constraints and coarse-grained models decrease the number of degrees of freedom

• Restricting degrees of freedom produces approximate dynamics